Basic Concepts - Rate of growth

It is not possible to perform simple analysis on the algorithm to determine exact amount of time required by it. The first complication is that the exact amount of time will depend on the implementation of the algorithm and on the actual machine. Another complication is that the time requirements will depend on the amount of input data. So the estimate for the time required by an algorithm is represented as a function of the size of the input data.

Suppose M is an algorithm and suppose n is the size of input data. The complexity function f(n) of M increases as n increases. The rate of increase of f(n) is found by comparing f(n) with some standard functions, such as:

log₂ n, n, n log₂ n, n², n³, 2ⁿ

Table for rate of growth of standard functions

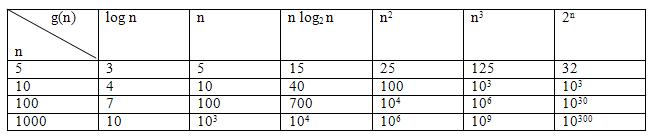
According to the above table, the rates of growth are: The logarithmic function log₂ n grows most slowly, the exponential function 2ⁿ grows most rapidly and the polynomial function n^c grows according to the exponent c.

Click here to go on website